The Second National Data Science Bowl, a data science competition where the goal was to automatically determine cardiac volumes from MRI scans, has just ended. We participated with a team of 4 members from Ghent University and finished 2nd!
The team kunsthart (artificial heart in English) consisted of Ira Korshunova, Jeroen Burms, Jonas Degrave, 3 PhD students, and professor Joni Dambre. It’s also a follow-up of last year’s team ≋ Deep Sea ≋, which finished in first place for the First National Data Science Bowl.
Overview
This blog post is going to be long, here is a clickable overview of different sections.
- Introduction
- Pre-processing and data augmentation
- Network architectures
- Training and ensembling
- Software and hardware
- Conclusion
Introduction
The problem
The goal of this year’s Data Science Bowl was to estimate minimum (end-systolic) and maximum (end-diastolic) volumes of the left ventricle from a set of MRI-images taken over one heartbeat. These volumes are used by practitioners to compute an ejection fraction: fraction of outbound blood pumped from the heart with each heartbeat. This measurement can predict a wide range of cardiac problems. For a skilled cardiologist analysis of MRI scans can take up to 20 minutes, therefore, making this process automatic is obviously useful.
Unlike the previous Data Science Bowl, which had very clean and voluminous data set, this year’s competition required a lot more focus on dealing with inconsistencies in the way the very limited number of data points were gathered. As a result, most of our efforts went to trying out different ways to preprocess and combine the different data sources.
The data
The dataset consisted of over a thousand patients. For each patient, we were given a number of 30-frame MRI videos in the DICOM format, showing the heart during a single cardiac cycle (i.e. a single heartbeat). These videos were taken in different planes including the multiple short-axis views (SAX), a 2-chamber view (2Ch), and a 4-chamber view (4Ch). The SAX views, whose planes are perpendicular to the long axis of the left ventricle, form a series of slices that (ideally) cover the entire heart. The number of SAX slices ranged from 1 to 23. Typically, the region of interest (ROI) is only a small part of the entire image. Below you can find a few of SAX slices and Ch2, Ch4 views from one of the patients. Red circles on the SAX images indicate the ROI’s center (later we will explain how to find it), for Ch2 and Ch4 they specify the location of SAX slices projected on the corresponding view.
sax_5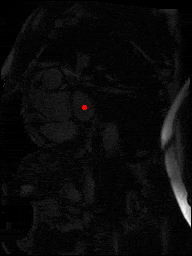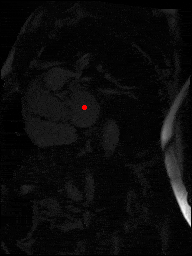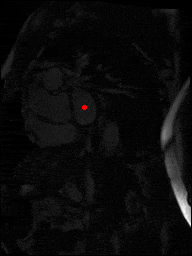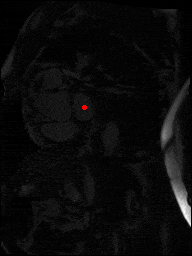 |
sax_9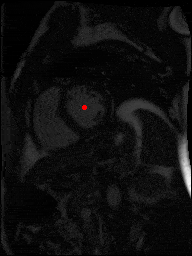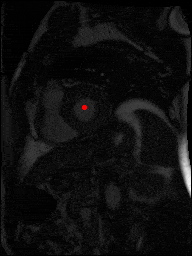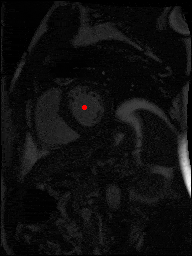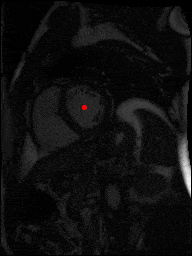 |
sax_10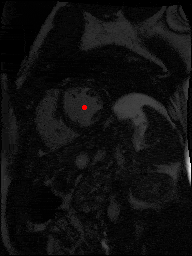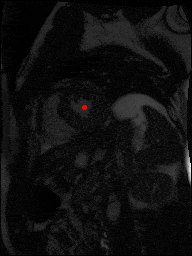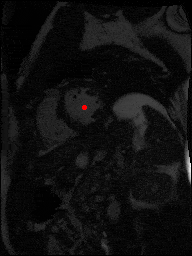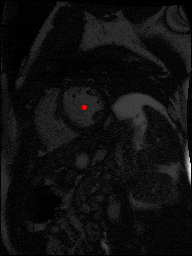 |
sax_11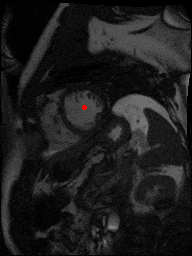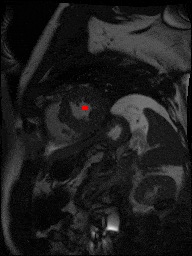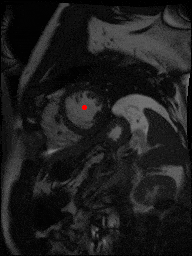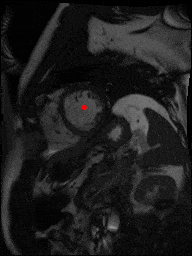 |
sax_12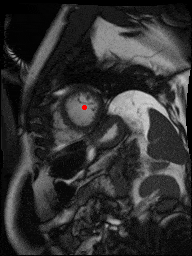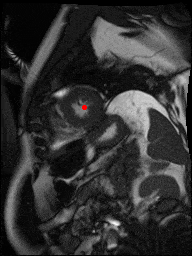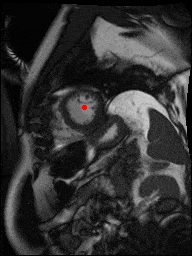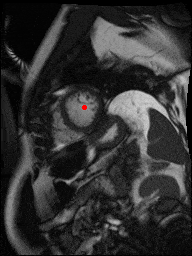 |
sax_15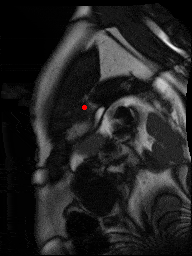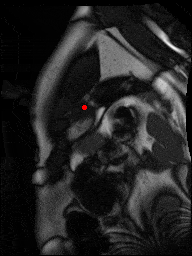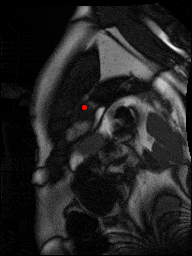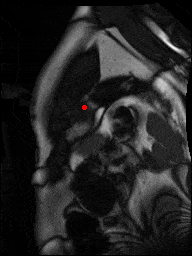 |
2Ch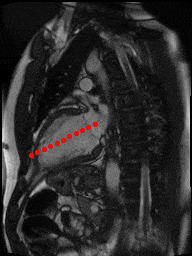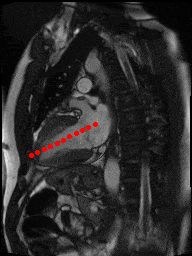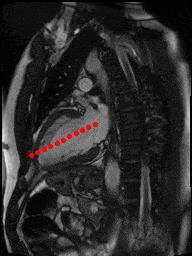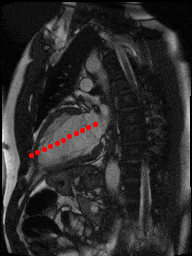 |
4Ch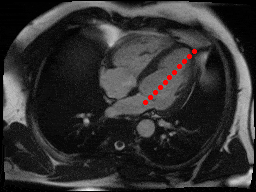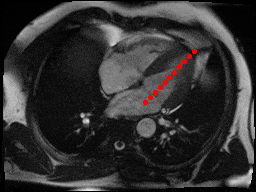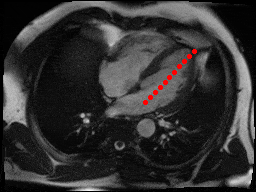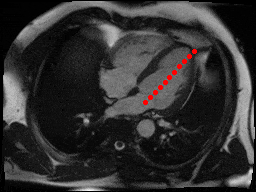 |
The DICOM files also contained a bunch of metadata. Some of the metadata fields, like PixelSpacing and ImageOrientationm were absolutely invaluable to us. The metadata also specified patient’s age and sex.
For each patient in the train set, two labels were provided: the systolic volume and the diastolic volume. From what we gathered (link), these were obtained by cardiologists by manually performing a segmentation on the SAX slices, and feeding these segmentations to a program that computes the minimal and maximal heart chamber volumes. The cardiologists didn’t use the 2Ch or 4Ch images to estimate the volumes, but for us they proved to be very useful.
Combining these multiple data sources can be difficult, however for us dealing with inconsistencies in the data was more challenging. Some examples: the 4Ch slice not being provided for some patients, one patient with less than 30 frames per MRI video, couple of patients with only a handful of SAX slices, patients with SAX slices taken in weird locations and orientations.
The evaluation
Given a patient’s data, we were asked to output a cumulative distribution function over the volume, ranging from 0 to 599 mL, for both systole and diastole. The models were scored by a Continuous Ranked Probability Score (CRPS) error metric, which computes the average squared distance between the predicted CDF and a Heaviside step function representing the real volume.
An additional interesting novelty of this competition was the two stage process. In the first stage, we were given a training set of 500 patients with a public test set of 200 patients. In the final week we were required to submit our model and afterwards the organizers released the test data of 440 patients and labels for 200 patients from the public test set. We think the goal was to compensate for the small dataset and prevent people from optimizing against the test set through visual inspection of every part of their algorithm. Hand-labeling in the first stage was allowed on the training dataset only, for the second stage it was also allowed for 200 validation patients.
The solution: traditional image processing, convnets, and dealing with outliers
In our solution, we combined traditional image processing approaches, which find the region of interest (ROI) in each slice, with convolutional neural networks, which perform the mapping from the extracted image patches to the predicted volumes. Given the very limited number of training samples, we tried combat overfitting by restricting our models to combine the different data sources in predefined ways, as opposed to having them learn how to do the aggregation. Unlike many other contestants, we performed no hand-labelling .
Pre-processing and data augmentation
The provided images have varying sizes and resolutions, and do not only show the heart, but the entire torso of the patient. Our preprocessing pipeline made the images ready to be fed to a convolutional network by going through the following steps:
- applying a zoom factor such that all images have the same resolution in millimeters
- finding the region of interest and extracting a patch centered around it
- data augmentation
- contrast normalization
To find the correct zooming factor, we made use of the PixelSpacing metadata field, which specifies the image resolution. Further we will explain our approach to ROI detection and data augmentation.
Detecting the Region Of Interest through image segmentation techniques
We used classical computer vision techniques to find the left ventricle in the SAX slices. For each patient, the center and width of the ROI were determined by combining the information of all the SAX slices provided. The figure below shows an example of the result.
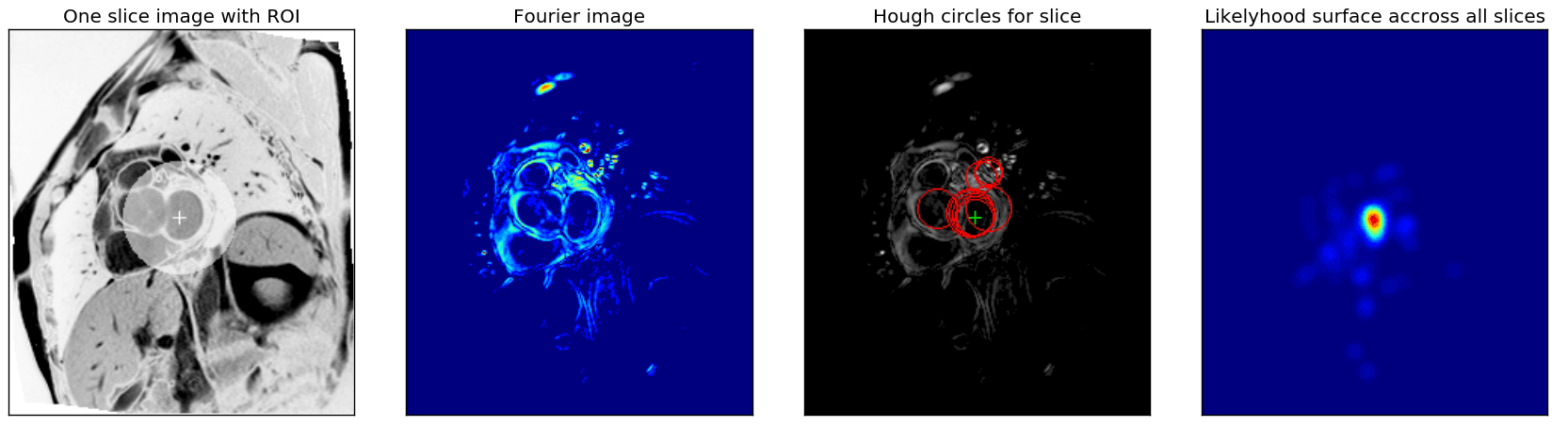
First, as was suggested in the Fourier based tutorial, we exploit the fact that each slice sequence captures one heartbeat and use Fourier analyses to extract an image that captures the maximal activity at the corresponding heartbeat frequency (same figure, second image).
From these Fourier images, we then extracted the center of the left ventricle by combining the Hough circle transform with a custom kernel-based majority voting approach across all SAX slices. First, for each fourier image (resulting from a single sax slice), the \(N\) highest scoring Hough circles for a range of radii were found, and from all of those, the \(M\) highest scoring ones were retained. \(N\), \(M\) and the range of radii are metaparameters that severely affect the robustness of the ROI detected and were optimised manually. The third image in the figure shows an example of the \(M\) best circles for one slice.
Finally, a ‘likelihood surface’ (rightmost image in figure above) was obtained by combining the centers and scores of the selected circles for all slices. Each circle center was used as the center for a Gaussian kernel, which was scaled with the circle score, and all these kernels were added. The maximum across this surface was selected as the center of the ROI. The width and height of the bounding box of all circles with centers within a maximal distance (another hyperparameter) of the ROI center were used as bounds for the ROI or to create an ellipsoidal mask as shown in the figure.
Given these ROIs in the SAX slices, we were able to find the ROIs in the 2Ch and 4Ch slices by projecting the SAX ROI centers onto the 2Ch and 4Ch planes.
Data augmentation
As always when using convnets on a problem with few training examples, we used tons of data augmentation. Some special precautions were needed, since we had to preserve the surface area. In terms of affine transformations, this means that only skewing, rotation and translation was allowed. We also added zooming, but we had to correct our volume labels when doing so! This helped to make the distirbution of labels more diverse.
Another augmentation here came in the form of shifting the images over the time axis. While systole was often found in the beginning of a sequence, this was not always the case. Augmenting this, by rolling the image tensor over the time axis, made the resulting model more robust against this noise in the dataset, while providing even more augmentation of our data.
Data augmentation was applied during the training phase to increase the number of training examples. We also applied the augmentations during the testing phase, and averaged predictions across the augmented versions of the same data sample.
Network architectures
We used convolutional neural networks to learn a mapping from the extracted image patches to systolic and diastolic volumes. During the competition, we played around a lot with both minor and major architectural changes. Our base architecture for most of our models was based on VGG-16.
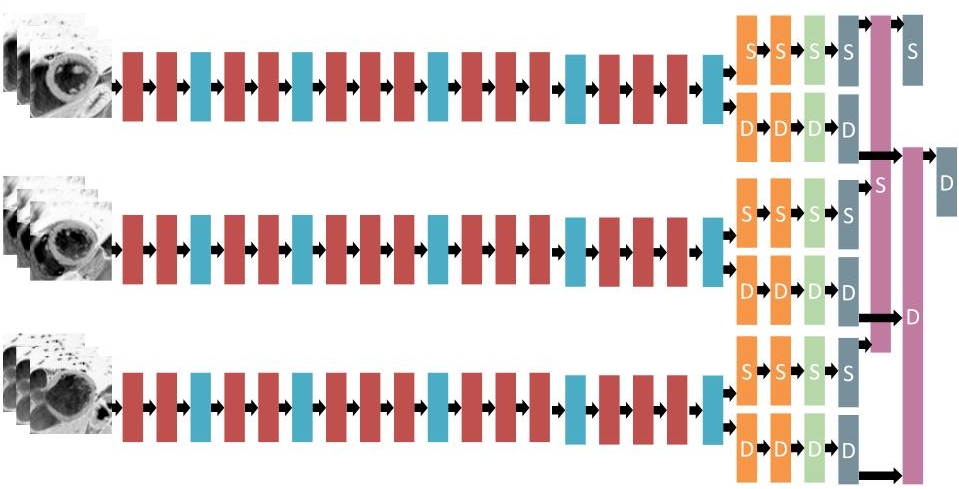
As we already mentioned, we trained different models which can deal with different kinds of patients. There are roughly four different kinds of models we trained: single slice models, patient models, 2Ch models and 4Ch models.
Single slice models
Single slice models are models that take a single SAX slice as an input, and try to predict the systolic and diastolic volumes directly from it. The 30 frames were fed to the network as 30 different input channels. The systolic and diastolic networks shared the convolutional layers, but the dense layers were separated. The output of the network could be either a 600-way softmax (followed by a cumulative sum), or the mean and standard deviation of a Gaussian (followed by a layer computing the cdf of the Gaussian).
Although these models obviously have too little information to make a decent volume estimation, they benefitted hugely from test-time augmentation (TTA). During TTA, the model gets slices with different augmentations, and the outputs are averaged across augmenations and slices for each patient. Although this way of aggregating over SAX slices is suboptimal, it proved to be very robust to the relative positioning of the SAX slices, and is as such applicable to all patients.
Our single best single slice model achieved a local validation score of 0.0157 (after TTA), which was a reliable estimate for the public leaderboard score for these models. The approximate architecture of the slice models is shown on the following figure.


2Ch and 4Ch models
These models have a much more global view on the left ventricle of the heart than single SAX slice models. The 2Ch models also have the advantage of being applicable to every patient. Not every patient had a 4Ch slice. We used the same VGG-inspired architecture for these models. Individually, they achieved a similar validation score (0.0156) as was achieved by averaging over multiple sax slices. By ensembling only single slice, 2Ch and 4Ch models, we were able to achieve a score of 0.0131 on the public leaderboard.
Patient models
As opposed to single slice models, patient models try to make predictions based on the entire stack of (up to 25) SAX slices. In our first approaches to these models, we tried to process each slice separately using a VGG-like single slice network, followed by feeding the results to an overarching RNN in an ordered fashion. However, these models tended to overfit badly. Our solution to this problem consists of a clever way to merge predictions from multiple slices. Instead of having the network learn how to compute the volume based on the results of the individual slices, we designed a layer which combines the areas of consecutive cross-sections of the heart using a truncated cone approximation.
Basically, the slice models have to estimate the area \(A_i\) (and standard deviation thereof) of the cross-section of the heart in a given slice \(i\). For each pair of consecutive slices \(i\) and \(i+1\), we estimate the volume of the heart between them as \(V_i = ⅓*h_{i, i+1}*(A_i + \sqrt{A_i A_{i+1}} + A_{i+1})\), where \(h_{i, i+1}\) is the distance between the slices. The total volume is then given by \(V = \sum_i V_i\).
Ordering the SAX slices and finding the distance between them was achieved through looking at the SliceLocation metadata fields, but this field was not very reliable in finding the distance between slices, neither was the SliceThickness. We looked for the two slices that were furthest apart, drew a line between them, and projected every other slice onto this line. This way, we estimated the distance between two slices ourselves.
Our best single model achieved a local validation score of 0.0105 using this approach. This was no longer a good leaderboard estimation, since our local validation set contained relatively few outliers compared to the public leaderboard in the first round. The model had the following architecture:

| Layer Type | Size | Output shape |
|---|---|---|
| Input layer | (8, 25, 30, 64, 64)* | |
| Convolution | 128 filters of 3x3 | (8, 25, 128, 64, 64) |
| Convolution | 128 filters of 3x3 | (8, 25, 128, 64, 64) |
| Max pooling | (8, 25, 128, 32, 32) | |
| Convolution | 128 filters of 3x3 | (8, 25, 128, 32, 32) |
| Convolution | 128 filters of 3x3 | (8, 25, 128, 32, 32) |
| Max pooling | (8, 25, 128, 16, 16) | |
| Convolution | 256 filters of 3x3 | (8, 25, 256, 16, 16) |
| Convolution | 256 filters of 3x3 | (8, 25, 256, 16, 16) |
| Convolution | 256 filters of 3x3 | (8, 25, 256, 16, 16) |
| Max pooling | (8, 25, 256, 8, 8) | |
| Convolution | 512 filters of 3x3 | (8, 25, 512, 8, 8) |
| Convolution | 512 filters of 3x3 | (8, 25, 512, 8, 8) |
| Convolution | 512 filters of 3x3 | (8, 25, 512, 8, 8) |
| Max pooling | (8, 25, 512, 4, 4) | |
| Convolution | 512 filters of 3x3 | (8, 25, 512, 4, 4) |
| Convolution | 512 filters of 3x3 | (8, 25, 512, 4, 4) |
| Convolution | 512 filters of 3x3 | (8, 25, 512, 4, 4) |
| Max pooling | (8, 25, 512, 2, 2) | |
| Fully connected (S/D) | 1024 units | (8, 25, 1024) |
| Fully connected (S/D) | 1024 units | (8, 25, 1024) |
| Fully connected (S/D) | 2 units (mu and sigma) | (8, 25, 2) |
| Volume estimation (S/D) | (8, 2) | |
| Gaussian CDF (S/D) | (8, 600) |
* The first dimension is the batch size, i.e. the number of patients, the second dimension is the number of slices. If a patient had fewer slices, we padded the input and omitted the extra slices in the volume estimation.
Oftentimes, we did not train patient models from scratch. We found that initializing patient models with single slice models helps against overfitting, and severely reduces training time of the patient model.
The architecture we described above was one of the best for us. To diversify our models, some of the good things we tried include:
- processing each frame separately, and taking the minimum and maximum at some point in the network to compute systole and diastole
- sharing some of the dense layers between the systole and diastole networks as well
- using discs to approximate the volume, instead of truncated cones
- cyclic rolling layers
- leaky RELUs
- maxout units
One downside of the patient model approach was that these models assume that SAX slices nicely range from one end of the heart to the other. This was trivially not true for patients with very few (< 5) slices, but it was harder to detect automatically for some other outlier cases as in figure below, where something is wrong with the images or the ROI algorithm fails.
sax_12 |
sax_15 |
sax_17 |
sax_36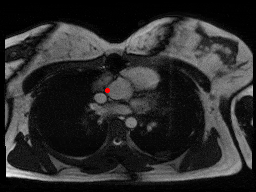 |
sax_37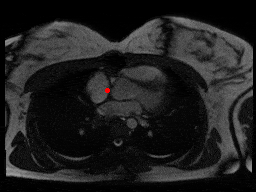 |
sax_41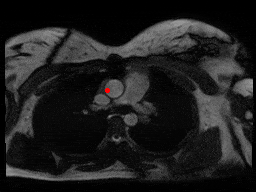 |
2Ch |
4Ch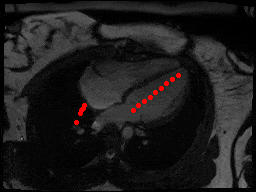 |
Training and ensembling
Error function. At the start of the competition, we experimented with various error functions, but we found optimising CRPS directly to work best.
Training algorithm. To train the parameters of our models, we used the Adam update rule (Kingma and Ba).
Initialization. We initialised all filters and dense layers orthogonally (Saxe et al.). Biases were initialized to small positive values to have more gradients at the lower layer in the beginning of the optimization. At the Gaussian output layers, we initialized the biases for mu and sigma such that initial predictions of the untrained network would fall in a sensible range.
Regularization. Since we had a low number of patients, we needed considerable regularization to prevent our models from overfitting. Our main approach was to augment the data and to add a considerable amount of dropout.
Validation
Since the trainset was already quite small, we kept the validation set small as well (83 patients). Despite this, our validation score remained pretty close to the leaderboard score. Also, in cases where it didn’t, it helped us identify issues in our models, namely problematic cases in the test set which were not represented in our validation set. We noticed for instance that quite some of our patient models had problems with patients with too few SAX slices (< 5).
Selectively train and predict
By looking more closely at the validation scores, we observed that most of the accumulated error was obtained by wrongly predicting only a couple of such outlier cases. At some point, being able to handle only a handful of these meant the difference between a leaderboard score of 0.0148 and 0.0132!
To mitigate such issues, we set up our framework such that each individual model could choose not to train on or predict a certain patient. For instance, models on patients’ SAX slices could choose not to predict patients with too few SAX slices, models which use the 4Ch slice would not predict for patients who don’t have this slice. We extended this idea further by developing expert models, which only trained and predicted for patients with either a small or a big heart (as determined by the ROI detection step). Further down the pipeline, our ensembling scripts would then take these non-predictions into account.
Ensembling and dealing with outliers
We ended up creating about 250 models throughout the competition. However, we knew that some of these models were not very robust to certain outliers or patients whose ROI we could not accurately detect. We came up with two different ensembling strategies that would deal with these kind of issues.
Our first ensembling technique followed the following steps:
- For each patient, we select the best way to average over the test time augmentations. Slice models often preferred a geometric averaging of distributions, whereas in general arithmetic averaging worked better for patient models.
- We average over the models by calculating each prediction’s KL-divergence from the average distribution, and the cross entropy of each single sample of the distribution. This means that models which are further away from the average distribution get more weight (since they are more certain). It also means samples of the distribution closer to the median-value of 0.5 get more weight. Each model also receives a model-specific weight, which is determined by optimizing these weights over the validation set.
- Since not all models predict all patients, it is possible for a model in the ensemble to not predict a certain patient. In this case, a new ensemble without these models is optimized, especially for this single patient. The method to do this is described in step 2.
- This ensemble is then used on every patient on the test-set. However, when a certain model’s average prediction disagrees too much with the average prediction of all models, the model is thrown out of the ensemble, and a new ensemble is optimized for this patient, as described in step 2. This meant that about ~75% of all patients received a new, ‘personalized’ ensemble.
Our second way of ensembling involves comparing an ensemble that is suboptimal, but robust to outliers, to an ensemble that is not robust to them. This approach is especially interesting, since it does not need a validation set to predict the test patients. It follows the following steps:
- Again, for each patient, we select the best way to average over the test time augmentations again.
- We combine the models by using a weighted average on the predictions, with the weights summing to one. These weights are determined by optimising them on the validation set. In case not all models provide a prediction for a certain patient, it is dropped for that patient and the weights of the other models are rescaled such that they again sum to one. This ensemble is not robust to outliers, since it contains patient models.
- We combine all 2Ch, 4Ch and slice models in a similar fashion. This ensemble is robust to outliers, but only contains less accurate models.
- We detect outliers by finding the patients where the two ensembles disagree the most. We measure disagreement using CRPS. If the CRPS exceeds a certain threshold for a patient, we assume it to be an outlier. We chose this threshold to be 0.02.
- We retrain the weights for the first ensemble, but omit the outliers from the validation set. We choose this ensemble to generate predictions for most of the patients, but choose the robust ensemble for the outliers.
Following this approach, we detected three outliers in the test set during phase one of the competition. Closer inspection revealed that for all of them either our ROI detection failed, or the SAX slices were not nicely distributed across the heart. Both ways of ensembling achieved similar scores on the public leaderboard. (0.0110)
Second round submissions
For the second round of the competition, we were allowed to retrain our models on the new labels (+ 200 patients). We were also allowed to plan two submissions. Of course, it was impossible to retrain all of our models during this single week. For this reason, we chose to only train our 44 best models, according to our ensembling scripts.
For our first submission, we splitted of a new validation set. The resulting models were combined using our first ensembling strategy.
For our second submission, we trained our models on the entire training set (i.e. there was no validation split). We assembled them using the second ensembling method. Since we had no validation set to optimise the weights of the ensemble, we computed the weights by training an ensemble on the models we trained with a validation split, and transferred them over.
Software and hardware
We used Lasagne, Python, Numpy and Theano to implement our solution, in combination with the cuDNN library. We also used PyCUDA for a few custom kernels. We made use of scikit-image for pre-processing and augmentation.
We trained our models on the NVIDIA GPUs that we have in the lab, which include GTX TITAN X, GTX 980, GTX 680 and Tesla K40 cards. We would like to thank Frederick Godin and Elias Vansteenkiste for lending us a few extra GPUs in the last week of the competition.
Conclusion
In this competition, we tried out different ways to preprocess data and combine information from different data sources, and thus, we learned a lot in this aspect. However, we feel that there is still a room for improvement. For example, we observed that most of our error still hails from a select group of patients. These include the ones for which our ROI extraction fails. In hindsight, hand-labeling the training data and training a network to do the ROI extraction would be a better approach, but we wanted to sidestep doing a lot of this kind of manual effort as much as possible. In the end, labeling the data would probably have been less time intensive.
UPDATE (March 23): the code is now available on GitHub: github.com/317070/kaggle-heart